Fourier Optics

Prof François Rigaut
Research School of Astronomy & Astrophysics
The Australian National University

© Rigaut 2021, PHYS3057 Fourier Optics

Linear Optical Systems

© Rigaut 2021, PHYS3057 Fourier Optics
Preamble
© Rigaut 2021, PHYS3057 Fourier Optics

Introduction: Sources

  • "Introduction to Fourier Optics and coherence", J.-M.Mariotti, in Diffraction limited imaging with very large telescope, editors D.M.Alloin and J.-M. Mariotti, 1988 (JMM),
  • "Introduction to Fourier Optics", Joseph Goodman, 2004 (JG)
  • "Fundamental of Photonics", B.E.A Saleh & M.C.Teich, 1991, mostly Chapter 4 (S&T),
  • "Principles of Optics", Max Born and Emil Wolf, 1980 (B&W),
  • "Computational Fourier Optics: A MATLAB Tutorial", David Voelz
  • The web, wikipedia.
© Rigaut 2021, PHYS3057 Fourier Optics

History of Fourier Optics

  • 1660: First observation of diffraction by Grimaldi
  • 1678: Huygens "Traité de la lumière" (published 1690): first wave theory of light. Require finite speed of light.
  • 1803: Thomas Young two slits interferences experiment.
  • 1818: Fresnel produces the first theory of diffraction.
  • 1822: Fourier introduces his transform
  • 1850-1950: Krichhoff, Sommerfeld, then Quantum Mechanics bring a firm mathematical foundation to the theory.
  • Of course Newton was involved too !
© Rigaut 2021, PHYS3057 Fourier Optics

Validity and limit conditions

  • Previous lectures from PHYS3057 were 1D optics, coherent (waveguides, lasers). The next lectures with me will be on 2D optics, incoherent sources (imaging).

  • We will consider light as a scalar field (B&W 8.4)

  • We’ll be focusing (pun intended) on Fraunhofer diffraction

  • Diffraction occurs with all waves, including sound, water, electromagnetic (X through radio), elementary particles.

  • We’ll browse through the maths, it is there for reference and those who’d like to dig deeper

© Rigaut 2021, PHYS3057 Fourier Optics

Next two lectures in one slide

  • Basic understanding of the Fourier transform and its properties, sampling and aliasing issues

  • In Fourier Optics, light is described by a scalar field Ψ=Aexp⁡iφ\Psi = A \exp^{i\varphi}

  • In Fraunhofer diffraction, the far and near field complex amplitudes are linked by a Fourier transform Ψ(P)=F(Ψ(M))\Psi(P) = {\cal F}(\Psi(M))

  • An optical system can be characterised by its impulse function HH. The impulse function is H=∣F(Ψ(x))∣2H = |{\cal F}\left(\Psi(x)\right)|^2

  • Object OO and image I{\cal I} are linked by the relation I=O∗H{\cal I} = O \ast H

  • The Optical Transfer Function of a system characterises its spatial frequencies filtering properties OTF=F(H)=Ψ∗Ψ⋆{\rm OTF} = {\cal F}(H) = \Psi \ast \Psi^\star

© Rigaut 2021, PHYS3057 Fourier Optics
Introduction to modal expansion
© Rigaut 2021, PHYS3057 Fourier Optics

Modal Expansion


f=∑iaiμi\Huge f = \sum_i a_i \mu_i

where:

  • ff is a discrete function/object
  • μi\mu_i are modes that you are going to use to represent
  • aia_i are the coefficients
© Rigaut 2021, PHYS3057 Fourier Optics

Modal expansion

  • The nature world is continuous
  • Once measured, a signal is discrete.
    • Volt versus time
    • Elevation map
    • Image
  • Chose the modal basis adapted to your problem.
  • Goal is to try to reduce the number of parameter to describe function, and make use of convenient properties of this description
  • Examples:
    • An optical phase using Zernike modes φ=∑iaiZi\varphi = \sum_i a_i Z_i
    • Finite Element Model analysis
    • Eigenvalues engenmodes
  • Cyclic signals are naturally described by expanding on sines and cosines →f=∑iaicos⁡(iθ)+bisin⁡(iθ)\rightarrow f = \sum_i a_i \cos(i\theta) + b_i \sin(i\theta)
© Rigaut 2021, PHYS3057 Fourier Optics
The Fourier Transform
© Rigaut 2021, PHYS3057 Fourier Optics

What is the Fourier Transform?

  • The Fourier transform of a signal tells you what frequencies are present in your signal and in what proportions
  • IMHO, the most useful mathematical tool for engineers and applied physicists.
  • It is used to:
    • Characterise signals (1D/2D..) and linear systems. Electronics, optics, acoustics, mechanics, civil engineering, etc, etc…
    • Digitally process data/signals (filtering, convolving, correlating, etc) in all above disciplines
© Rigaut 2021, PHYS3057 Fourier Optics

Fourier Filtering

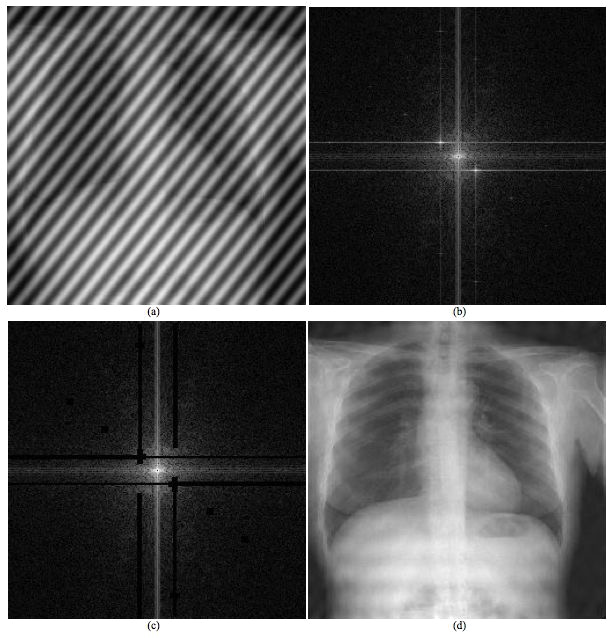
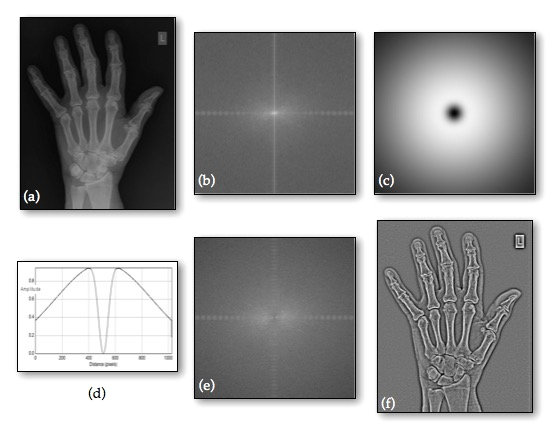
© Rigaut 2021, PHYS3057 Fourier Optics

Fourier transform: definitions

  • We note f^\hat{f} the Fourier transform of ff

f^(u)=∫−∞+∞f(x)exp⁡−i2πuxdx\hat{f}(u) = \int_{-\infty}^{+\infty} f(x) \exp^{-i2\pi ux} dx

  • The inverse Fourier transform is f(x)=∫−∞+∞f^(u)exp⁡+i2πuxduf(x) = \int_{-\infty}^{+\infty} \hat{f}(u) \exp^{+i2\pi ux} du
  • We will also use the Fourier operator F{\cal F}: f^(u)=F[f(x)]\hat{f}(u) = {\cal F}[f(x)]
  • The Fourier transform is cyclic: F−1[F[f(x)]]=f(x){\cal F}^{-1}[{\cal F}[f(x)]] = f(x)
  • To have a Fourier transform, a function must
    • Be absolutely integrable

    ∣∫−∞+∞f(x)dx∣<∞\small \left| \int_{-\infty}^{+\infty} f(x) dx \right| < \infty

    • Not have any infinite discontinuity
    • Have only a finite number of discontinuities or extrema in any finite interval
© Rigaut 2021, PHYS3057 Fourier Optics

Fourier Pairs



Function Fourier Pair
exp⁡(−πx2)\exp(-\pi x^2) exp⁡(−πu2)\exp(-\pi u^2)
sinc(x){\rm sinc}(x) Π(u)\Pi(u)
sinc2(x){\rm sinc}^2(x) Λ(u)\Lambda(u)
δ(x)\delta(x) 11
III(x){\rm III}(x) III(u){\rm III}(u)
sin⁡(πx)\sin(\pi x) i2δ(u+12)−i2δ(u−12)\frac{i}{2} \delta (u+\frac{1}{2}) - \frac{i}{2} \delta (u-\frac{1}{2})
© Rigaut 2021, PHYS3057 Fourier Optics

Properties

Property Expression
Linearity if h(x)=af(x)+bg(x)→h^(u)=af^(u)+bg^(u)h(x) = a f(x) + b g(x) \rightarrow \hat{h}(u) = a \hat{f}(u) + b \hat{g}(u)
Similarity F[f(ax)]=1∣a∣f^(ua){\cal F}[f(ax)] = \frac{1}{ \lvert a \rvert } \hat{f} \left( \frac{u}{a} \right)
Shift F[f(x−a)]=e−i2πauf^(u){\cal F}[f(x-a)] = e^{-i2\pi a u} \hat{f}(u)
Convolution F[f(x)∗g(x)]=F[f(x)]×F[g(x)]=f^(u)×g^(u){\cal F}[f(x)\ast g(x)] = {\cal F}[f(x)] \times {\cal F}[g(x)] = \hat{f}(u) \times \hat{g}(u)
Autocorrel. F[f(x)∗f(x)]=∣f^(u)∣2{\cal F}[f(x)\ast f(x)] = \lvert \hat{f}(u) \rvert^2
Parseval ∫−∞+∞f(x)×g∗(x)dx=∫−∞+∞f^(u)×g^∗(u)du\int_{-\infty}^{+\infty} f(x) \times g^\ast(x) dx = \int_{-\infty}^{+\infty} \hat{f}(u) \times \hat{g}^\ast(u) du
Power ∫−∞+∞∣f(x)∣2dx=∫−∞+∞∣f^(u)∣2du\int_{-\infty}^{+\infty} \lvert f(x) \rvert^2 dx = \int_{-\infty}^{+\infty} \lvert \hat{f}(u) \rvert^2 du
Derivative F[ddxf(x)]=i2πuf^(u){\cal F}\left[ \frac{d}{dx} f(x) \right] = i2\pi u \hat{f}(u)
© Rigaut 2021, PHYS3057 Fourier Optics
2D FT, DFT, FFT, PSD
  • Acronyms:
    • FT: Fourier Transform
    • DFT: Discrete FT
    • FFT: Fast FT
    • PSD: Power Spectral Density (modulus square)
© Rigaut 2021, PHYS3057 Fourier Optics

2D Fourier transform

The Forward transform is:

f^(u,v)=∬−∞+∞f(x,y)e−i2π(ux+vy)dxdy\hat{f}(u,v) = \iint_{-\infty}^{+\infty} f(x,y) e^{-i2\pi (ux+vy)} dx dy

And the Reverse is

f(x,y)=∬−∞+∞f^(u,v)e+i2π(ux+vy)dudvf(x,y) = \iint_{-\infty}^{+\infty} \hat{f}(u,v) e^{+i2\pi (ux+vy)} du dv


  • Note that if ff can be factorised (convenient) f(x,y)=g(x).h(y)f(x,y) = g(x).h(y) then f^(u,x)=g^(u)×h^(v)\hat{f}(u,x) = \hat{g}(u) \times \hat{h}(v)
    • (but if f(x,y)=g(r).h(θ)f(x,y) = g(r).h(\theta) the problem is more complicated ...)
  • All other theorems apply as in 1D (linearity, similarity, power, etc)
© Rigaut 2021, PHYS3057 Fourier Optics

Some 2D Fourier pairs

© Rigaut 2021, PHYS3057 Fourier Optics

Discrete FT and Fast FT

  • The Fourier transform can be modified for discrete datasets, which is extremely useful to represent and analyse sampled physical signals. The discrete Fourier transform (DFT) is:

f^(ν)=1N∑τ=0N−1f(τ)e−i2πντ/Nf(τ)=∑ν=0N−1f^(ν)e+i2πντ/N\begin{aligned} \hat{f}(\nu) & = \frac{1}{N} \sum_{\tau=0}^{N-1} f(\tau) e^{-i2\pi\nu\tau/N} \\ f(\tau) & = \sum_{\nu=0}^{N-1} \hat{f}(\nu) e^{+i2\pi\nu\tau/N} \end{aligned}

  • τ\tau and ν\nu are discrete variables. Both functions consist of sequences of N samples. Basic theorems for the FT also apply to the DFT.
  • The Fast Fourier Transform (FFT) is a DFT that uses a smart algorithm to drastically reduce the number of operations, from N2N^2 down to Nlog⁡(N)N \log(N)
© Rigaut 2021, PHYS3057 Fourier Optics

The Power Spectral Density (PSD)

  • The square modulus of the Fourier transform of a signal

PSD(f)=∣F(f(x))∣2{\rm PSD}(f) = |{\cal F}(f(x))|^2

  • PSD is insensitive to the phase of the input signal.
    • you get the power (intensity) per frequency bin over the frequency range 0 to cut off frequency
  • In a DFT, assuming:
    • the units of x are seconds (s),
    • and the units of f, say, Volts (V)
    • then the PSD units are V2^2/Hz.

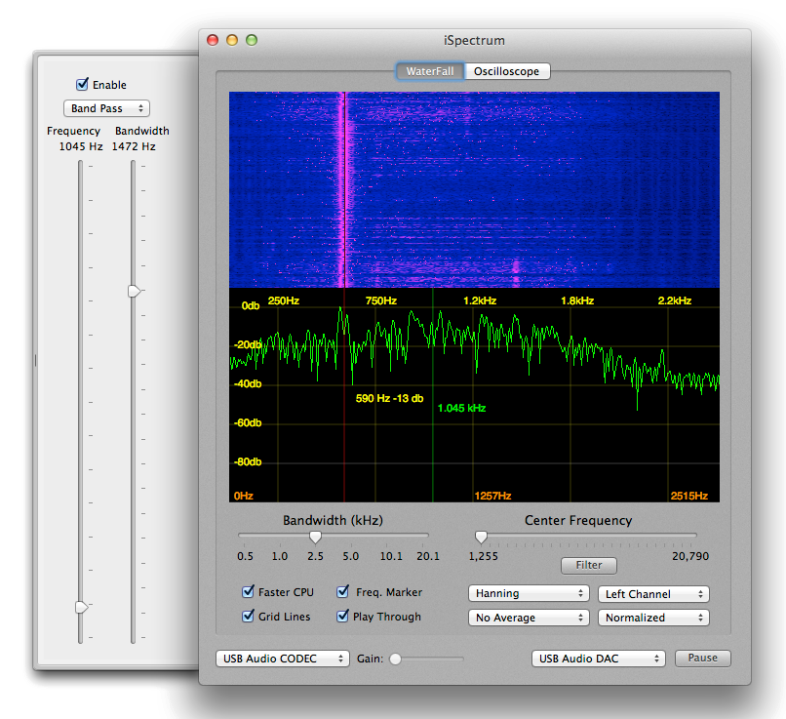
See Spectrum Density Analyser

© Rigaut 2021, PHYS3057 Fourier Optics
Diffraction Theory
© Rigaut 2021, PHYS3057 Fourier Optics

Huygens Principle

  • "Every point on a wavefront may be considered a source of secondary spherical wavelets which spread out in the forward direction at the speed of light. The new wavefront is the tangential surface to all of these secondary wavelets."
© Rigaut 2021, PHYS3057 Fourier Optics

(Non) Derivation of the diffracted field
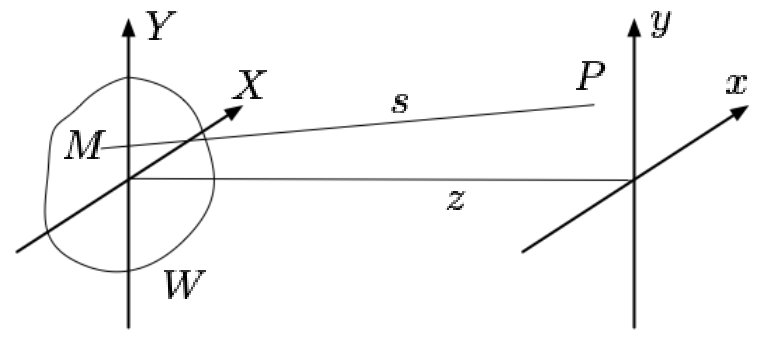  • Fresnel, KrichHoff and Sommerfeld, within others, have worked out the math. It's messy, and requires a lot of approximations.
  • Applying the Huygens principle and working out the field propagation from the point P0P_0 through the aperture WW in plan MM (near field), to the final plan PP (far field), it can be demonstrated that the field in PP is the simple Fourier Transform of the field in MM:

Ψ(P)=F(Ψ(M))\Large \Psi (P) = {\cal F}(\Psi (M))

© Rigaut 2021, PHYS3057 Fourier Optics
Wavefront, PSF, OTF
© Rigaut 2021, PHYS3057 Fourier Optics

The Impulse Function

  • Recalling the field in P: Ψ(P)=F(Ψ(M))\Psi(P) = {\cal F}(\Psi(M))
  • At visible wavelengths, it is extremely difficult to measure the complex field itself (for quantum noise reasons) - but we can measure the field intensity (irradiance), the square of the complex field. H is the image of a point, the impulse function, also called the Point Spread Function (PSF):

H=Ψ(P).Ψ∗(P)=F(Ψ(M)).F∗(Ψ(M))=∣F(Ψ(M))∣2H = \Psi(P).\Psi^\ast(P) = {\cal F}(\Psi(M)).{\cal F}^\ast(\Psi(M)) = |{\cal F}(\Psi(M))|^2

Remember that Ψ=Aeiφ\Psi = A e^{i \varphi}? So, in absence of aberrations (φ≡0\varphi\equiv0), we simply have:

H=∣F(A)∣2H = | {\cal F}(A) |^2

© Rigaut 2021, PHYS3057 Fourier Optics

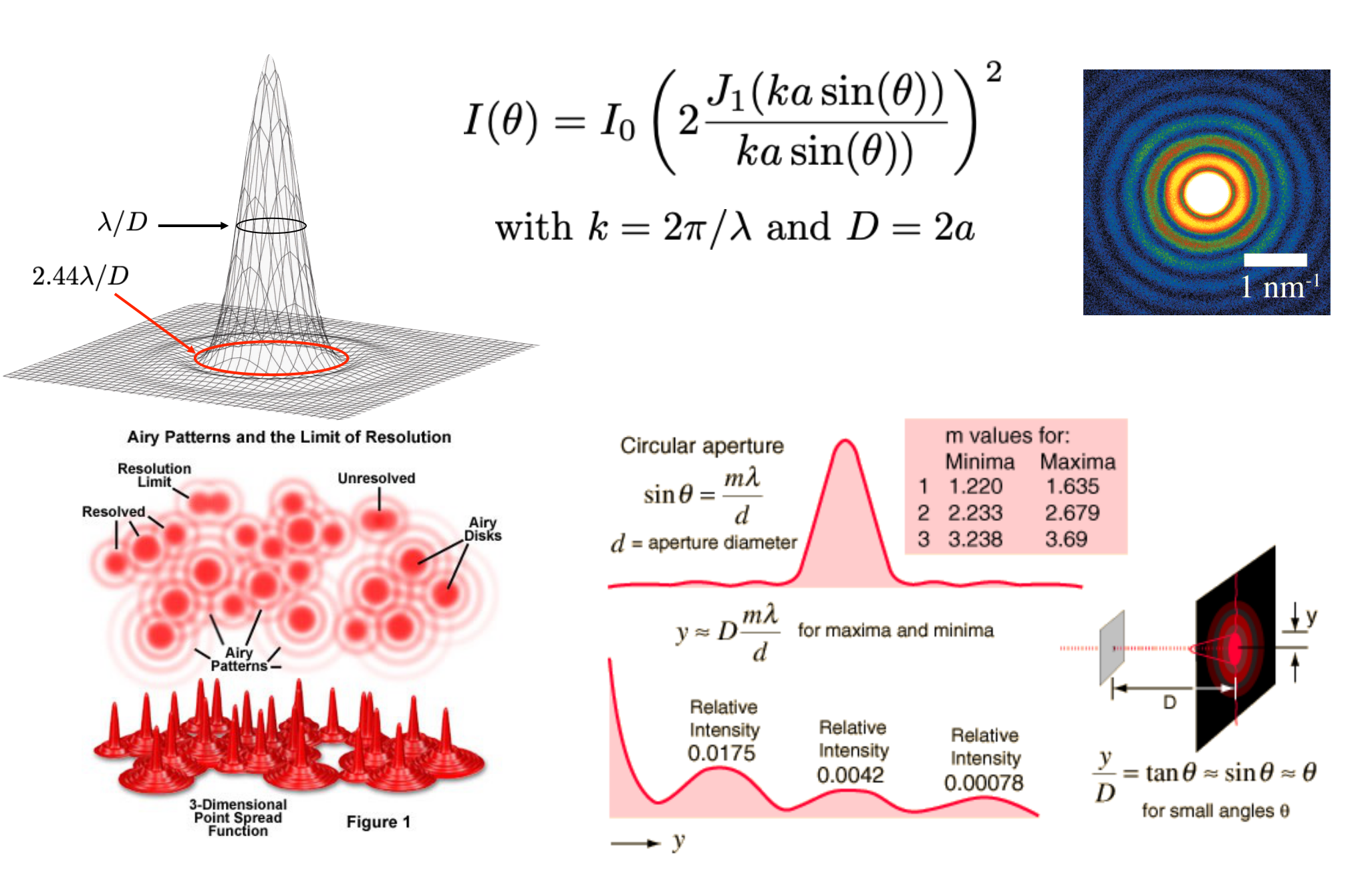
The Impulse Function, circular aperture

For a circular aperture:

Ψ(M)=Ψ(r,θ)=Π(r2a)={1if r≤a0if r>a \Psi(M) = \Psi(r,\theta) = \Pi \left(\frac{r}{2a} \right) = \begin{cases} 1 &\text{if } r\le a \\\\ 0 &\text{if } r > a \end{cases}

H=∣F(Ψ(M))∣2=∣F(Ψ(Π(r/2a)))∣2=[aJ1(2πaρ)ρ]2H = | {\cal F}(\Psi(M))|^2 = | {\cal F}(\Psi(\Pi (r/2a)))|^2 = \left[ a \frac{J_1(2\pi a \rho)}{\rho} \right]^2

© Rigaut 2021, PHYS3057 Fourier Optics

An Application: Young Fringes

  • Armed with this new mathematical description of diffraction, it is now trivial to find, e.g., the expression of the Young fringes.

  • The 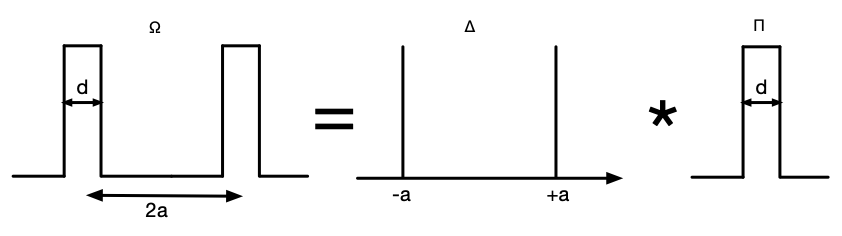slits can be described as a convolution:

  • The near field can be written Ω(x)=Δ(x/a)∗Π(x/d)\small \Omega(x) = \Delta(x/a) \ast \Pi(x/d)

  • The far field is Ω^(u)=F(Δ(x/a)∗Π(x/d))=F(Δ(x/a))×F(Π(x/d))\small \hat{\Omega}(u) = {\cal F}(\Delta(x/a) \ast \Pi(x/d)) = {\cal F}(\Delta(x/a)) \times {\cal F}(\Pi(x/d))

  • Δ(x/a)=δ(x−a)+δ(x+a)\small \Delta(x/a) = \delta(x-a)+\delta(x+a) hence
    F(Δ(x/a))=e−i2πau+e+i2πau=2cos⁡(2πau)\small {\cal F}(\Delta(x/a)) = e^{-i2\pi au}+e^{+i2\pi au} = 2 \cos(2\pi au)

  • and F(Π(x))=sinc(u)\small {\cal F}(\Pi(x)) = {\rm sinc}(u) hence F(Π(x/d))=sinc(ud)\small {\cal F}(\Pi(x/d)) = {\rm sinc}(ud)

Thus Ω^(u)=2cos⁡(2πau)×sinc(ud)\small \hat{\Omega}(u) = 2 \cos(2\pi au) \times {\rm sinc}(ud) and the intensity (measured)

∣Ω^(u)∣2=4cos⁡2(2πau)×sinc2(ud)|\hat{\Omega}(u)|^2 = 4 \cos^2(2\pi au) \times {\rm sinc}^2(ud)

© Rigaut 2021, PHYS3057 Fourier Optics

Airy pattern, circular aperture PSF

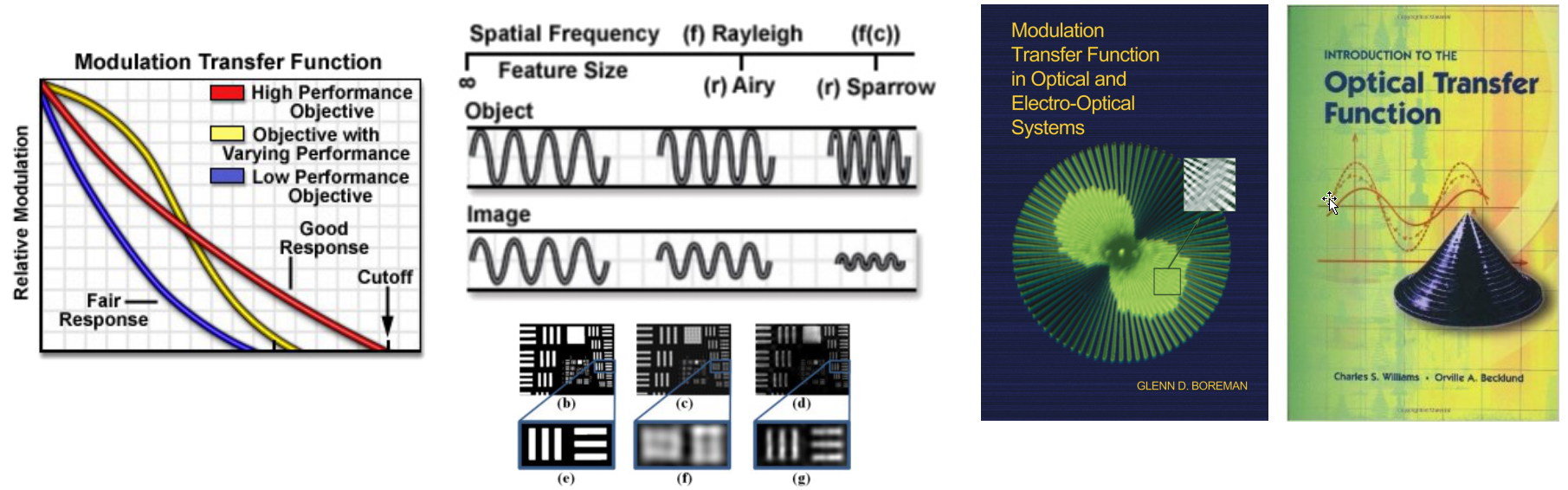
© Rigaut 2021, PHYS3057 Fourier Optics

The Optical Transfer Function

  • Also called generically Modulation Transfer Function (MTF)

OTF=∣F(H)∣=∣Ψ∗Ψ∗∣{\rm OTF} = |{\cal F}(H)| = |\Psi \ast \Psi^*|

  • Characterises the filtering properties of an optical system, including cut-off frequency
  • For a circular aperture, the cut-off frequency is fc=D/λf_c = D/\lambda
  • People have written books about it…
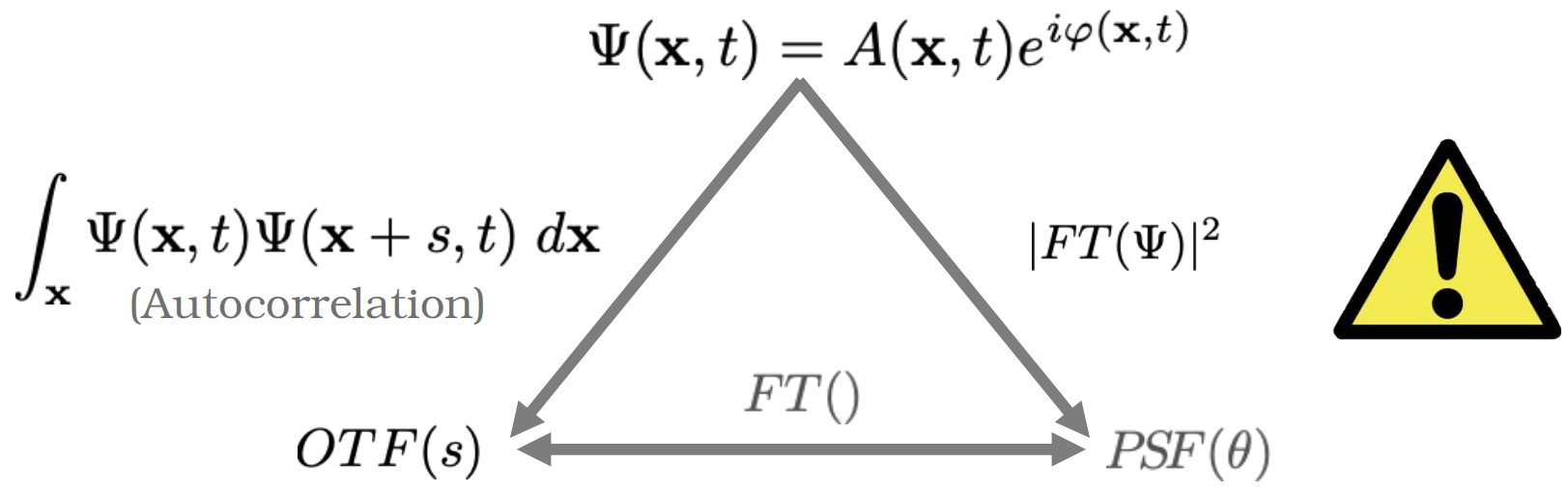
© Rigaut 2021, PHYS3057 Fourier Optics

Wavefront, PSF & OTF are linked

  • The wavefront is Ψ(x,y,t)=A(x,y,t)exp⁡(iφ(x,y,t))\Psi(x,y,t) = A(x,y,t) \exp( i \varphi(x,y,t))
    • Ψ\Psi is the complex field defined by its amplitude and phase
    • AA is the amplitude (e.g. pupil function)
    • φ\varphi is the phase
  • The Optical Transfer Function (or MTF) is the spatial frequency response of the system.
  • Wavefront, PSF and OTF are linked:
© Rigaut 2021, PHYS3057 Fourier Optics
Interferometry to Imaging
...and Back
© Rigaut 2021, PHYS3057 Fourier Optics

Image formation for incoherent sources

An object O can be decomposed into an infinite number of dirac function. In the case of an incoherent object (most objects in everyday’s life, astronomical objects, medicine,etc), these points do not interfere, thus the resulting image is the convolution of the object and the impulse response (PSF)

I=O−H\Large {\cal I} = O - H

Note that this assumes invariance of PSF with position in the field of view.

© Rigaut 2021, PHYS3057 Fourier Optics

Interferometry to Imaging...

From "slit" to full aperture

Near field
= Aperture
= Pupil
Far field
= Focal plane Image
Image cross section
© Rigaut 2021, PHYS3057 Fourier Optics

Interferometry to Imaging...

From "slit" to full aperture

© Rigaut 2021, PHYS3057 Fourier Optics

Interferometry to Imaging...

From "slit" to full aperture

© Rigaut 2021, PHYS3057 Fourier Optics

Interferometry to Imaging...

From "slit" to full aperture

© Rigaut 2021, PHYS3057 Fourier Optics

Interferometry to Imaging...

From "slit" to full aperture

© Rigaut 2021, PHYS3057 Fourier Optics

Interferometry to Imaging...

From "slit" to full aperture

© Rigaut 2021, PHYS3057 Fourier Optics

Interferometry to Imaging...

From "slit" to full aperture

© Rigaut 2021, PHYS3057 Fourier Optics

Interferometry to Imaging...

From "slit" to full aperture

© Rigaut 2021, PHYS3057 Fourier Optics

... and Imaging to Interferometry

© Rigaut 2021, PHYS3057 Fourier Optics

... and Imaging to Interferometry

© Rigaut 2021, PHYS3057 Fourier Optics

... and Imaging to Interferometry

© Rigaut 2021, PHYS3057 Fourier Optics

... and Imaging to Interferometry

© Rigaut 2021, PHYS3057 Fourier Optics

... and Imaging to Interferometry

© Rigaut 2021, PHYS3057 Fourier Optics

... and Imaging to Interferometry

© Rigaut 2021, PHYS3057 Fourier Optics

... and Imaging to Interferometry

© Rigaut 2021, PHYS3057 Fourier Optics
Elements of Sampling Theory
© Rigaut 2021, PHYS3057 Fourier Optics

Sampling & Aliasing (Shannon/Nyquist)




If a continuous, band-limited function f(x)f(x) contains no frequency component higher than fcf_c, then it can be fully specified by a set of samples at frequency of 2×fc2\times f_c or larger.

© Rigaut 2021, PHYS3057 Fourier Optics

Sampling and the Shah function

III{\rm III} is also called a frequency comb.

  1. III(x){\rm III}(x) is its own Fourier transform

  2. The act of sampling is taking value at discrete points ≡\equiv Multiplication by III{\rm III}

© Rigaut 2021, PHYS3057 Fourier Optics

Aliasing

  • Can
    be spatial, temporal, angular, etc
  • Can be solved/mitigated by pre-filtering the signal before sampling
© Rigaut 2021, PHYS3057 Fourier Optics

The Shah function (part 2)



Convolution by III{\rm III} is equivalent to creating an infinite number of shifted replicas of the original functions

© Rigaut 2021, PHYS3057 Fourier Optics

Aliasing

Fourier view: In the DFT/FFT space, the function spectrum is replicated at intervals 2×fc2\times f_c. If the spectrum spills over ±fc\pm f_c, then the spectrum replicas will overlap, resulting in a mixed signal (original lost).

© Rigaut 2021, PHYS3057 Fourier Optics

proof of the sampling theorem

From f(x)f(x) we obtain the sampled fs(x)f_s(x) with sampling interval τ\tau by:

fs(x)=III(xτ).f(x)f_s(x) = {\rm III}\left(\frac{x}{\tau}\right).f(x)

In the Fourier domain:

fs^(u)=τ  III(τu)∗f^(u)=τ∑−∞+∞f^(u−nτ)\hat{f_s} (u) = \tau \; {\rm III}(\tau u) \ast \hat{f}(u) = \tau \sum_{-\infty}^{+\infty} \hat{f}\left( u - \frac{n}{\tau}\right)

The spectrum of the sampled function consists of an infinite sum of replicas of f^(u)\hat{f}(u). If τ−1<2fc\tau^{-1} < 2 f_c, the replicas are separated by distances larger than their width and do not overlap (if not, they do and it creates in aliasing). Hence the information on f^(u)\hat{f}(u) and thus on f(x)f(x) is preserved if the sampling condition τ≤1/(2fc)\tau \le 1/(2 f_c) is met. We can retrieve the original spectrum by multiplying f^(u)\hat{f}(u) by a rectangle function (gate) Π(τu)\Pi(\tau u) in order to eliminate all replicas but one:

[τ  III(τu)∗f^(u)]×Π(τu)=f^(u)\left[ \tau \; {\rm III}(\tau u) \ast \hat{f}(u) \right] \times \Pi(\tau u) = \hat{f}(u)

which yields by inverse Fourier transform

[III(x/τ).f(x)]∗τ−1sinc(x/τ)=fs(x)∗τ−1III(x/τ)=f(x)\left[ {\rm III}(x/\tau).f(x) \right] \ast \tau^{-1} {\rm sinc}(x/\tau) = f_s(x) \ast \tau^{-1} {\rm III}(x/\tau) = f(x)

© Rigaut 2021, PHYS3057 Fourier Optics
© Rigaut 2021, PHYS3057 Fourier Optics

Main points of past two lectures

  • Basic understanding of the Fourier transform and its properties, sampling and aliasing issues

  • In Fourier Optics, light is described by a scalar field Ψ=Aexp⁡iφ\Psi = A \exp^{i\varphi}

  • In Fraunhofer diffraction, the far and near field complex amplitudes are linked by a Fourier transform Ψ(P)=F(Ψ(M))\Psi(P) = {\cal F}(\Psi(M))

  • An optical system can be characterised by its impulse function HH. The impulse function is H=∣F(Ψ(x))∣2H = |{\cal F}\left(\Psi(x)\right)|^2

  • Object OO and image I{\cal I} are linked by the relation I=O∗H{\cal I} = O \ast H

  • The Optical Transfer Function of a system characterises its spatial frequencies filtering properties OTF=F(H)=Ψ∗Ψ⋆{\rm OTF} = {\cal F}(H) = \Psi \ast \Psi^\star

© Rigaut 2021, PHYS3057 Fourier Optics
Image Metrics, Aberations
© Rigaut 2021, PHYS3057 Fourier Optics

Practical Optical Systems

© Rigaut 2021, PHYS3057 Fourier Optics

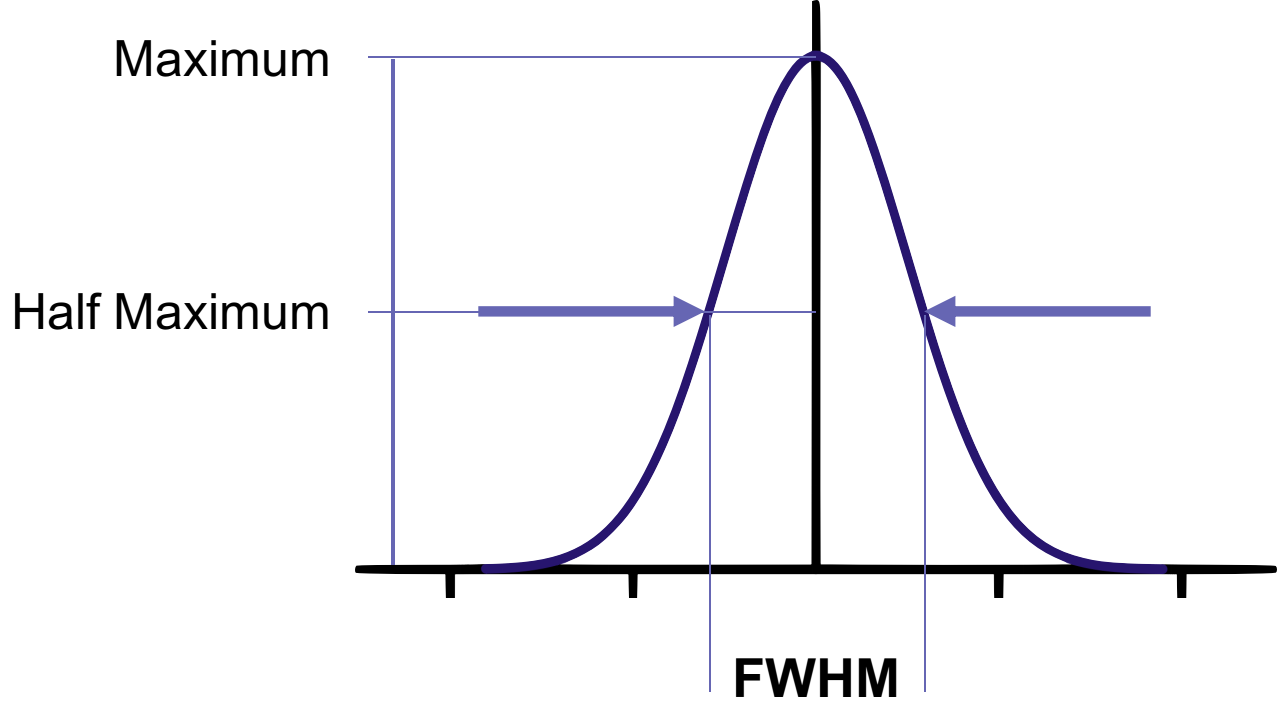
Image metric: Full-Width at Half-Maximum

  • The width of the image at half its maximum. Often written FWHM
  • For instance, a cross section of a gaussian image
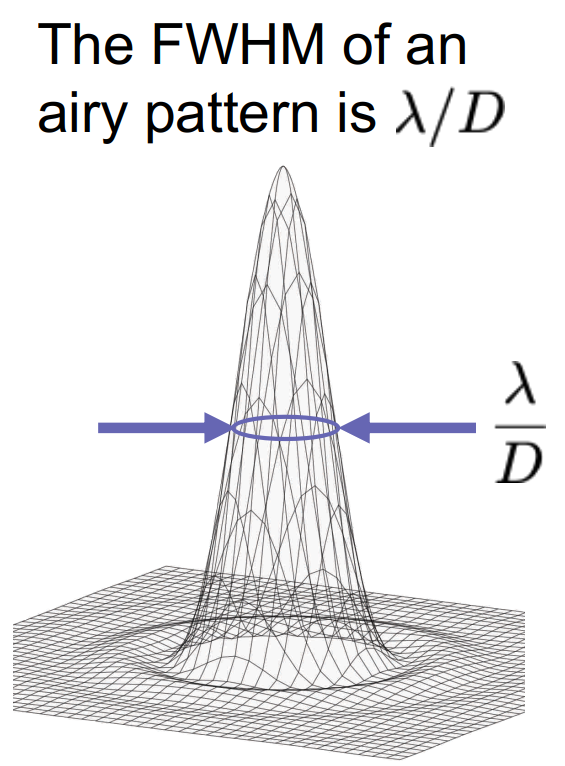
  • The FWHM is often naturally expressed as an angle (e.g. arcsec) or a distance (e.g. mm), as it often characterise a resolution
© Rigaut 2021, PHYS3057 Fourier Optics

Image metric: Strehl ratio

  • The ratio between the maximum intensity in the actual image to the maximum in a diffraction limited image.
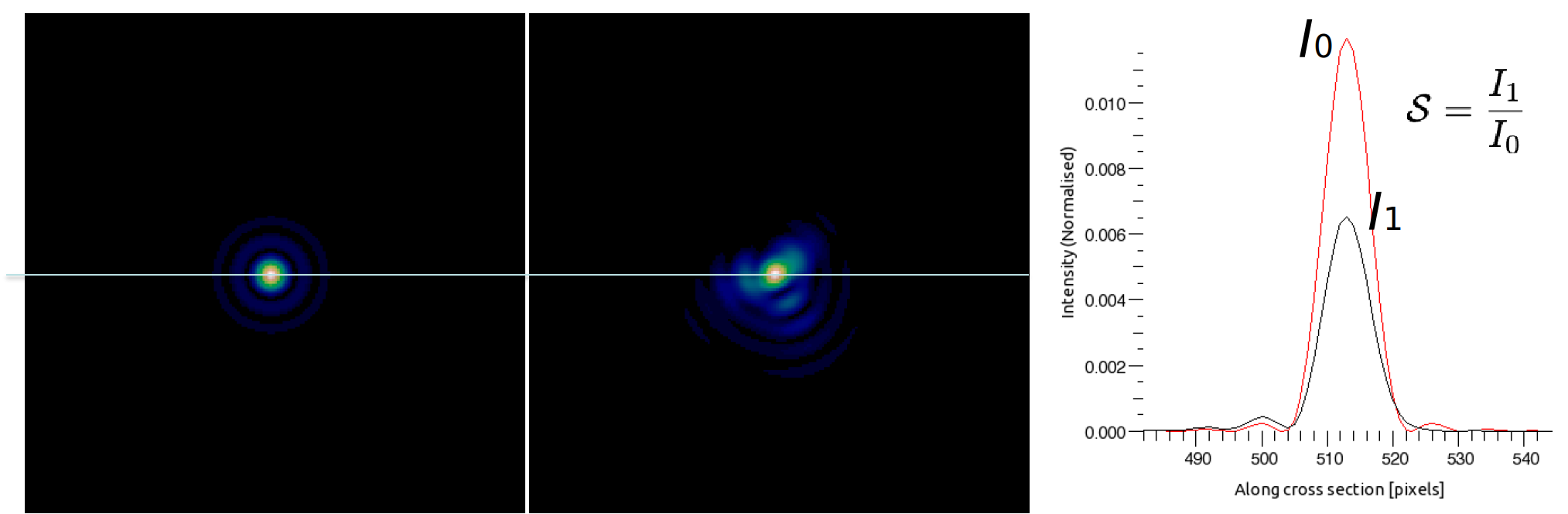
  • A measure of how much energy is in the diffraction limited core
  • For S≥0.2, S=exp⁡(−σφ2){\cal S} \ge 0.2 \text{, } {\cal S} = \exp(-\sigma^2_\varphi)
  • 0≤S≤10 \le {\cal S} \le 1. The Strehl ratio is often expressed in % (0<S<1000 < {\cal S} < 100%)

σφ2=1S∬S(φ(x,y)−φˉ)2ds is the phase variance\sigma^2_\varphi = \frac{1}{S} \iint_S \left( \varphi(x,y) - \bar{\varphi} \right)^2 ds \text{ is the phase variance}

© Rigaut 2021, PHYS3057 Fourier Optics

Image metric: Encircled Energy

  • Intensity within a certain radius normalised by total intensity of the image

ε(r)=∫θ=02π∫ρ=0rI(ρ,θ)ρ dρ dθ∫θ=02π∫ρ=0∞I(ρ,θ)ρ dρ dθ\varepsilon(r) = \frac{ \int_{\theta=0}^{2\pi}\int_{\rho=0}^{r} {\cal I}(\rho,\theta) \rho \: d\rho \: d\theta }{ \int_{\theta=0}^{2\pi}\int_{\rho=0}^{\infty} {\cal I}(\rho,\theta) \rho \: d\rho \: d\theta}

© Rigaut 2021, PHYS3057 Fourier Optics

Beyond "Simple" Metrics

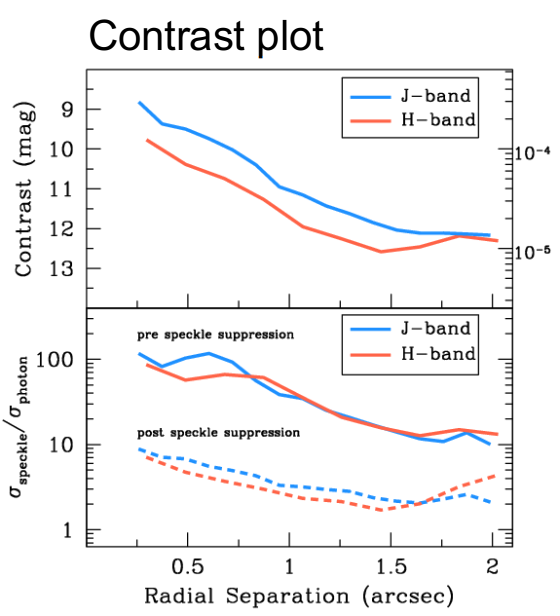
  • High
       HD8375. J.Crepp et al 2013   HR8799. T.Currie et al 2012
    contrast imaging required the development of new metrics and new techniques to improve contrast performance
  • Speckle control
© Rigaut 2021, PHYS3057 Fourier Optics

<div style="position: absolute; top:460px; left:35px;z-index:1;">Near field<br>= Aperture<br>= Pupil</div> <div style="position: absolute; top:460px; left:335px;">Far field<br>= Focal plane Image</div> <div style="position: absolute; top:460px; left:645px;">Image cross section</div>