


float shift(2); // WFS X/Y shift in pixels (it's shift first, rotation after). Set "use_fftshift" to use FFT method to shift. A positive shift value moves the WFS (ulens array) toward positive values in the pupil coordinate system (i.e. the pupil illumination moves opposite) float rotation; // WFS rotation in degrees (CCW). Set "use_fftrotate" to use FFT method to rotate.I have also included a couple of new parfiles in examples: sh16x16_wfsrot.par and mcao_wfsrot.par. In there, for instance:
wfs(1).rotation = 30.; // degrees CCW of rotation ot this WFS wfs(1).shift = [3,1]; // in pixelsNote that in the display, the WFS spots are not rotated, it is the phase and amplitude that are rotated, so the rotation of e.g. the DM appears CW in the display (but the WFS is indeed rotated CCW). Enjoy the new feature. This could bring interesting gains in tomographic systems.
I just pushed version 5.0 to github. The main changes with respect to the previous 4.9 version is
This work has mostly been motivated by the need for faster ELT simulations. I am now using it for GMT simulations, 6 LGS WFS, each of them 60x60 subapertures with 10 arcsec field of view, elongated LGS, physical image formation, all that at 6 iterations/seconds using yao w/ svipc on a 4 core hyperthreaded laptop (retina Macbook Pro). That means 100000 subapertures/seconds.
Here is the printout of test-all.i:
Tue Oct 16 12:15:55 2012 Parfile Name iter/s Display? Strehl test Simple SH6x6 w/ TT mirror, full... 117.0 ON 0.35@1.65mic test Simple SH6x6 w/ TT mirror, full... 126.6 OFF 0.35@1.65mic test1 Simili Altair LGS, full diffrac... 69.6 ON 0.59@1.65mic test1 Simili Altair LGS, full diffrac... 81.6 OFF 0.60@1.65mic test2 SH 12x12, quick method, with se... 391.4 ON 0.79@1.65mic test2 SH 12x12, quick method, with se... 513.4 OFF 0.79@1.65mic test3 GLAO example, 3 8x8 SHWFS, w/ d... 48.9 ON 0.05@2.23mic test3 GLAO example, 3 8x8 SHWFS, w/ d... 62.0 OFF 0.05@2.23mic test4 Simple Curvature 36 actuators w... 583.8 ON 0.56@2.20mic test4 Simple Curvature 36 actuators w... 874.0 OFF 0.56@2.20mic test5 2.5 metre telescope w/ Pyramid WFS 61.5 ON 0.84@2.20mic test5 2.5 metre telescope w/ Pyramid WFS 63.2 OFF 0.84@2.20mic test6 DH WFS & DM 585.9 ON 0.49@1.65mic test6 DH WFS & DM 997.6 OFF 0.49@1.65mic test7 LGS SH12x12, Extended WFS (11 n... 27.1 ON 0.50@1.65mic test7 LGS SH12x12, Extended WFS (11 n... 27.8 OFF 0.51@1.65mic test8 Simple SH6x6 w/ TT mirror, full... 1018.9 ON 0.47@1.65mic test8 Simple SH6x6 w/ TT mirror, full... 2002.0 OFF 0.47@1.65micSo that the simple geometrical SH6x6 now runs at 2000 it/s, and the curvature-36 is getting close to 1000 it/s. Part of this is Moore's law, and part are further optimizations of the code. On the feature side, there is now a more complete model of SHWFS that allows to define independently field of view, field stop size and spotpitch, as illustrated in this sketch:
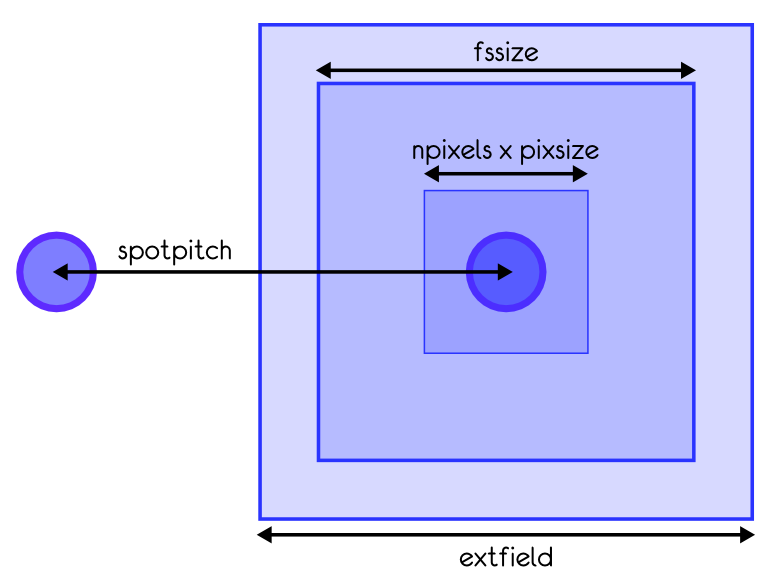
The definition is all backward compatible, so your old parfiles should not be affected.
One new interesting feature gained by Shack-Hartmann WFS is the so called "extended field" capability (wfs.extfield [arcsec]). Here is how it works: Up to now the subaperture field of view was wfs.pixsize*wfs.npixels. This was limited to a certain value, namely wfs.lambda/pupil_plane_pixel_size_in_meter, constrained by the laws of the FFT. For instance at 500nm and with 10cm per pixel in the pupil plane, you get one arcsec field of view. Period. This limits still applies with the new model, but now this 1x1 arcsec "imagelet" is embedded into a larger image, with shifts computed from the average input tilt in front of the given subaperture (of course the said tilt is removed from the input phase as it is effectively taken care of by the shift). This opens the possibility of much larger dynamical ranges without having to use a very large number of pixels in the input pupil. As far as turbulence goes, this also relieves the constraint of having 2-3 pixels per r0: Now that tip-tilt is "removed" before doing the FFT to compute the subaperture spot, the wrapping limit of 2pi per pixel is pushed further away (about 3 times further if we trust Noll, as the Tip-tilt-removed Noll residual is 13% of the phase variance, thus 36% in rms). Thus one can now safely go to one pixel per r0 before hitting the wrapping/aliasing limit on the image formation in each subaperture. This means 2 times lower sim.pupildiam are needed, and typically translate into a factor of 4 gain in speed (trust me, more on that in a later post). I hope that makes sense.
git clone git@github.com:frigaut/yao.git yao
The new parallel features (see next post), and especially the new sparse reconstructor options (see 2 posts below) makes running very large systems much more tractable than before. A 100x100 Shack-Hartmann system (on a 400 pixels pupil) runs at 8 iterations/seconds on an 8 core Xeon-based machine @ 3.33GHz! So one can get statiscally meaningful results in a few mn. It's not too greedy in RAM either (in modern machine standard) at 120MB for the main process (our machine has 8GB of RAM).
A 64x64 system runs at 23 iterations/s and a 200x200 SHWFS at 1 iterations/s (note that the later starts to be in the realm of ELT extreme AO, at 15cm actuator pitch on a 30-m).
More work on yao parallel:
8 Core Xeon (2 boards) @ 3.33GHz, running RHEL 5, 32 bits. yorick/yao built with -O2. 16x16 SHWFS system, physical model, no noise. All times (avg & median) in milliseconds for one frame. sh16x16_svipc: 1 threads, sh_wfs() avg=2.86, median=2.90 sh16x16_svipc: 2 threads, sh_wfs() avg=1.87, median=1.89 sh16x16_svipc: 4 threads, sh_wfs() avg=1.37, median=1.37 sh16x16_svipc: 8 threads, sh_wfs() avg=1.14, median=1.15 sh16x16_svipc: 16 threads, sh_wfs() avg=2.33, median=2.30You can see that the speed increases up to 8 forks (max gain = 2.5x). Adding more forks makes the thing slower. The gain does not reach larger value just because (1) there are overheads associated to the use of shared memory/semaphores and (2) there is also a global overhead in the sh_wfs() function. What's parallelize is the core of sh_wfs() (FFTs, noise application and slopes calculations from spots), but any overhead within the sh_wfs() function itself, before calling the FFT/slopes calculation routine is not going to gain from the parallelization.
The gain brought by the other, more general parallel features (DM/WFS & PSFs) is nicely illustrated by the following examples. This was run on the same machine (8 cores Xeon), with curvature.par (36 subapertures curvature system ran on a 120 pixels pupil). Look at the following results (I have omitted the timing results for items that are not of concerned here and were negligible):
sim.svipc=0 (no parallelization) time(1-2) = 9.89 ms (WF sensing) time(3-4) = 0.01 ms (cMat multiplication) time(4-5) = 1.04 ms (DM shape computation) time(5-6) = 5.84 ms (Target PSFs estimation) 59.18 iterations/second in average sim.svipc=1 (WFS/DM parallelized) time(1-2) = 4.11 ms (WF sensing) time(3-4) = 0.01 ms (cMat multiplication) time(4-5) = 0.94 ms (DM shape computation) time(5-6) = 5.78 ms (Target PSFs estimation) 91.43 iterations/second in average sim.svipc=2 (PSFs parallelized) time(1-2) = 10.69 ms (WF sensing) time(3-4) = 0.01 ms (cMat multiplication) time(4-5) = 1.05 ms (DM shape computation) time(5-6) = 1.23 ms (Target PSFs estimation) 76.41 iterations/second in average
That's a typical example. The "no parallel" case is dominated by WFSing (10ms) and PSF (6ms) calculations. When parallelizing the WFS (sim.svipc=1), the WFSing time goes down to 4ms. Indeed, now 6ms of it can be done in parallel with other tasks: here, the PSF calculation that takes 6ms. With sim.svipc=2 (only the PSF are parallelized), the PSF calculation time goes to basically to 0 while the WFSing stays at 10ms. It all makes sense. I haven't put the sim.svipc=3 results as they are a little more difficult to understand and would just introduce confusion.
The individual WFS parallel feature is controlled by the parameter wfs.svipc. The "global" DMs/WFSs abd PSF parallelization is controlled by sim.svipc (bit 0 controls DM/WFS and bit 1 controls PSFs, thus sim.svipc=3 means both are turned on).
Of course, if you want to use yao parallel facilities, you will need to install the yorick-svipc plugin (contributed by Matthieu Bec), through most of the normal channels. It runs on Linux (extensively tested) and OsX (somewhat tested).
Marcos van Dam (flatwavefronts.com), who is using yao to simulate the GMT AO system, has contributed a patch that add MMSE control matrices, with a couple of regularization (identity or laplacian) and a sparse option. The sparse makes it blazingly fast (both the inversion and the reconstruction show more than an order of magnitude speed gain).
Aurea Garcia-Rissmann (UofA), adapting code developed Mark Milton (at the time at UofA), contributed a new modal basis for the DMs: the disk harmonics. These represent well the kind of deformation produced by deformable secondaries, for instance. They are much better behaved than the Zernike at the edge.
Thanks Marcos and Aurea. The code was very clean, hence -relatively- easy to merge.
Following the development here at Gemini of a svipc plugin (by Matthieu Bec), providing shared memory capabilities for yorick, I have been working on parallelizing yao. The results so far are encouraging. For instance, I get a 4x performance boost on simulation of our MCAO system here, from 12 it/s to 47 it/s on an 8 core Xeon machine. This will of course work better for systems with multiple WFS and/or DMs, but will probably also bring some improvements for simpler systems.
Right now, I have implemented this in our version of yao that we forked to accomodate our special MCAO needs. But the functions are rather generic and I do not foresee major hurdles in porting that to the main yao tree. I just need to get a few free hours... So stay tuned!
I have come to develop yao once more. Version 4.5.0 brings a lot of new features, bug fixes and code re-organization. Here is the changelog:
Upgrades:Bug Fixes:
So, as you see, lots of new things. I apologize to those who knew well the yao code and for who this release is going to mean some work to find where the functions have gone, but I think the code re-organization was way overdue, and the results is cleaner. Many of these modifications were the results of a visit from Michael Hart (and some push from Marcos van Dam) to use yao for GMT simulations. As usual, I have benefited from many discussions, advices and code contribution from Damien Gratadour, Benoit Neichel, Yann Clenet and Eric Gendron.
Things I have missed in this release but that I firmly intend to implement in the next version:
Is the performance of today's computer still following Moore's law? If so, if I take my numbers of the section performance, that date back to 2004, we should get for the fastest case (sh6m2-bench.par) 170*2^5 = 5540 it/sec. That is not the case, but I re-run recently some tests on typical cases and I am happy to announce that the threshold of 1000 iterations/second has been passed. Here are some performance numbers, obtained on a MacBook Pro 17" (running Snow Leopard, aka 10.6.1, 2.66GHz, 4GB RAM, 64bits yorick and plugins). All simulations were runs with 4 phase screens, and the display on, unless noted otherwise. Results are in iterations/second.
| Name | case | 64bits | 32bits |
| shfast | SH 6x6 geometrical, 1DM+TT, NGS, 1 screen, no display | 1020 | 860 |
| test1 | SH 12x12 physical 1DM+TT, LGS | 44 | 32 |
| test2 | SH 12x12 geometrical, 1DM+TT, NGS | 219 | 182 |
| test3 | SH 6x6 physical 1DM+TT, NGS | 201 | 165 |
| test4 | CWFS36, NGS | 226 | 164 |
| test4bis | same, no display | 261 | 184 |
| sh20 | SH 20x20 geometrical, 1DM+TT, NGS, 1 screen, no display | 284 | N/A |
| sh20_2 | SH 20x20, physical, 1 screen, w/ display | 59 | N/A |
Those are all, I believe, fairly impressive numbers. Because I acquired this macbook only recently, I was doing comparison between a 32bits and 64bits yorick. Hence the last column of the table. Building/running in 64bits actually makes a fairly big difference on Snow Leopard. In average, the 64 bit version is 25% faster than the 32 bits one (up to 42% faster in some cases). That's a big gain.
I got several requests recently to help install yao on OsX (I believe the yao packages have been built for 10.5, so I don't think the following would work for Tiger 10.4). So, I wrote up some fairly detailled instructions. Here is the drill. Note that I do not believe that there is any pre-requisite (beside X11 of course). I tested that on a fresh test account in my mac and it worked. FFTW comes bundled with the yao package, so it is not necessary to install it.
Note: in fact, the following should also work on linux. Just select
the appropriate OS in pkg_setup when asked for it.
export PATH=$HOME/yorick-2.1.05/bin:$PATH
pkg_mngr.i is now bundled with yorick. So just do the
following (for
pkg_setup: all
defaults are good, so carriage return everywhere, except you will have to
select the OS: darwin-i686 on modern apple machines)
$ yorick #include "pkg_mnr.i" > pkg_setup > pkg_sync > pkg_list > pkg_install,"yao" > quit
$ cd ~ $ mkdir -p .yorick/data $ cd .yorick/data $ yorick -i turbulence.i > require,"yao.i" > CreatePhaseScreens,2048,256,prefix="screen" > quit $ ls ( you should have your screens)
$ cd ~/yorick-2.1.05/share/yao/examples/That's where some example yao parfile are. you can then put them wherever you want and transform/adapt them at will.
$ yorick -i yao.i > aoread,"sh6x6.par" > aoinit,disp=1 > aoloop,disp=1 > gowatch it go :-)
I know many people have had problems installing yao with the newest yorick releases. Since the yorick Makefile system has been re-hauled in fact. Well, many things have changed. Now you can install yao *very* easily from the yorick prompt. Just download the brand new binary plugin installer (require yorick > 1.6.02). To install the latest yao, just:
#include "pkg_mngr.i" pkg_list pkg_install,"yao"
beware that the install directive will install in yorick/contrib/yao, so if you have there an existing installation that you want to preserve, you should back it up before.
This yao version is kind of intermediary. I have not included all modifications from ralf. I have however made a fairly decent size change to aoloop:
Now aoloop is in 2 parts:aoloop,parameters_as_beforeto "load" the thing. then type
goor
go,1to run a single iteration.
While it's going, you now still have access to the prompt. You can type "stop" or "cont" to stop/resume the loop simulations.
If you write batches in which you run loops, you will have to write it like this:
aoloop,bla-bla-bla for (j=1;j<=loop.niter;j++) go;This is because a call to go goes only through one loop cycle, and then call "set_idler,go", which tells to the yorick interpreter "if you have nothing pending, run 'go'". This will work as intended when ran interactively, but when in a batch, the interpreter is not idle: it will execute directly the next line and will never go back to "go" if not forced to (hence the explicit loop).
Note added August 2: Indeed Ralf has been very active. He is in the final phases of testing and has been revamping major parts of yao to be compatible with the new reconstructor choices. Reconstructors will very soon include MAP, MAP+PCG, on top of the existing SVD/least square. Note that this will also include a sparse implementation, so it's fast !
Below is the excerpt of the README file relevant to this release:
We are now at version 3.2.3, which fixes a few bugs:
Ralf submitted many bug reports/comments. Miska pointed out a bug in create_phase_screens, linked to SIGFPE being triggered by a division by zero. I did not see the problem on my G4 (I should have seen it on the G5 but did not bother going thru the phase screen creation phase there). I have patched the problem in turbulence.i and put the new release on the web pages.
I have added some test parfiles in the examples directory (yao/examples). New users can test their distribution by running #include "test-all.i" in this directory. It's relatively fast, and test various configs (SHWFS method 1 and 2, with splitted subsystem, and a CWFS case).
Y_SITE/contrib/yao/.